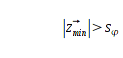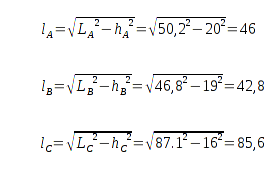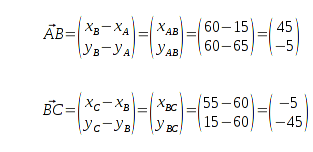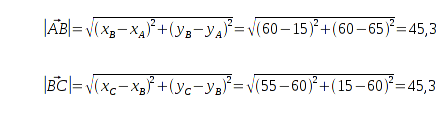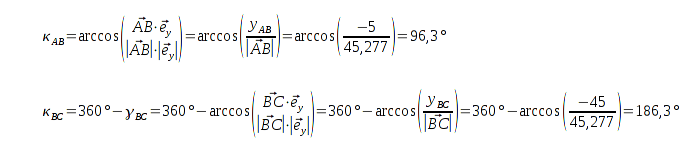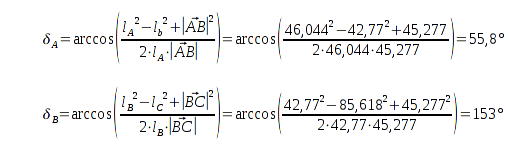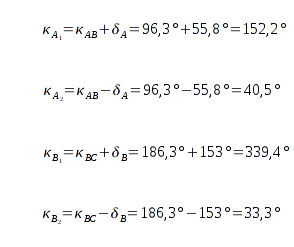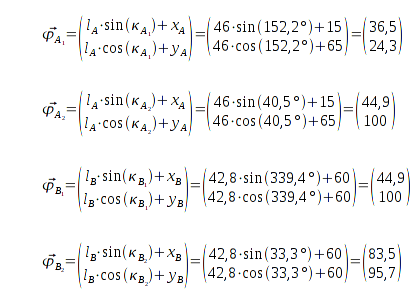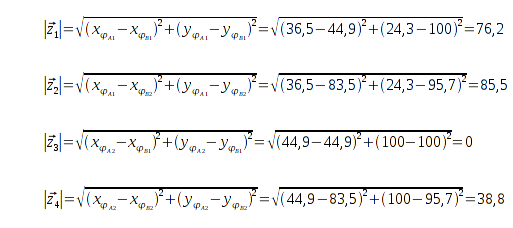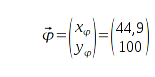Zusammenfassung der Standortbestimmung
Zusammenfassung der Standortbestimmung
- Die Betrachtung der Ausgangssituation

- Die Aufgabenstellung

- Die Auswahl dreier geeigneter Baken

- Messung der Abstände zu drei Baken und Projektion dieser in die Ebene

- Die Konstruktion eines Hilfsdreiecks

- Das Problem der zwei Lösungen für die Winkelbestimmung

- Die Berechnung eines zweiten Lösungspaares

- Ausschluss der falschen Lösungen

- Grafische Aufbereitung der Herleitung

- Eine Beispielrechnung



 Die Betrachtung der Ausgangssituation
Die Betrachtung der Ausgangssituation
Das Gebiet, in dem sich der Bot befindet, ist ein Garten. Trotz geringer Unebenheiten betrachte ich ihn der Einfachheit halber als eine Ebene, die durch ein zweidimensionales kartesisches Koordinatensystem dargestellt werden kann. Der Koordinatenursprung ist dabei so gewählt, daß er außerhalb des Gartens liegt und dieser sich vollständig im positiven Quadranten befindet. Dies ist schon für die Planung zur Rasterkarte relevant und wird dort betrachtet.
Ich habe für mich festgelegt, daß alle absoluten Winkel, also z.b. von Vektoren oder durch Motoransteuerung durchgeführte Drehungen, auf die y-Achse des Koordinatensystems bezogen sind und mit dem Uhrzeigersinn steigen. Dadurch entsteht eine Analogie zu den Himmelsrichtungen und der Kompassrose. Diese Betrachtung entspricht nicht den Konventionen bezüglich Polarkoordinaten. Tatsächlich habe ich überlegt, mit einem Polarkoordinatensystem zu arbeiten, dies aber dann verworfen, weil dann wieder die Umrechnung in Rasterkarten komplizierter wird.
An mehreren Orten sind Navigationsbaken (A, B, C, ...) aufgestellt. Sie sind vom φ unterscheid- und einzeln ansprechbar und er kennt ihre Positionen in der Ebene und ihre Höhen.
 |


 Die Aufgabenstellung
Die Aufgabenstellung
Der Bot hat die nötige Sensorik, um mittels Laufzeitmessung den Abstand zu den Baken zu bestimmen. Ziel ist, einen Algorithmus zu entwickeln, der aus den Laufzeitmessungen die Roboterposition berechnen kann. Als Referenzen dienen die fixen Positionen der Baken im Raum.
Die Aufgabe ist gelöst, wenn der Bot einen Vektor 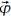 bestimmt hat, der vom Ursprung auf seine Position zeigt.
bestimmt hat, der vom Ursprung auf seine Position zeigt.
In der folgenden Grafik ist die Bake A als Referenz, sowie die unbekannte Botposition dargestellt.
Wäre der Vektor
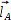
bekannt, so könnte die Position des Roboters leicht berechnet werden:
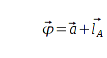
Ziel ist es nun,
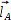
zu berechnen.
Hierfür benötigt der Bot zu Beginn drei Abstandsmessungen.


 Die Auswahl dreier geeigneter Baken
Die Auswahl dreier geeigneter Baken
Der Bot muss sich also drei sinnvolle Baken herauspicken, mit denen die Position bestimmt werden soll. Beginnt er von Null, ist dies ein Sprung ins kalte Wasser. Er hat keinerlei Annahmen über den Bereich, in dem er sich befindet. Deshalb beginnt er einen Rundumscan und sucht alle Baken, die er erreichen kann, und mißt deren Abstände. Hat er mehr als drei gefunden, muss er selektieren. Beim Scannen kann der Bot schon erste Tendenzen über die Richtungen erkennen, da seine Sensorik Richtcharakteristik hat. Es erhöht die Genauigkeit, wenn Baken, die in ähnlicher Richtung liegen, nicht gleichzeitig zu einer Berechnung herangezogen werden. Eine mittlere Entfernung verspricht ebenfalls höhere Genauigkeit. Hier muss dem Bot ein geeigneter Algorithmus mitgegeben werden, der allerdings an anderer Stelle diskutiert wird.
Informationen über geeignete Baken könnten auch in der Rasterkarte abgelegt sein, sodaß mein φ gezielter und schneller zu Abstandsdaten kommen könnte.
In der folgenden Betrachtung sei angenommen, der Bot habe sich bereits für die drei Baken A, B und C als sinnvolle Konstellation entschieden.


 Messung der Abstände zu drei Baken und Projektion dieser in die Ebene
Messung der Abstände zu drei Baken und Projektion dieser in die Ebene
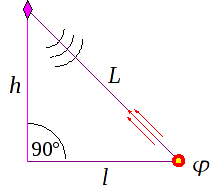
Ich betrachte hier den Bot φ und eine Nav-Bake. Mittels Laufzeitmessung bestimmt der Bot zu der Bake die Entfernung L und projeziert den Abstand in die Ebene. Dies geschieht dank Pythagoras sehr einfach:
Ich habe es hier augenscheinlich mit einem rechtwinkligen Dreieck zu tun, und da entspricht die gemessene Entfernung
L der Hypothenuse und die Bakenhöhe
h einer Kathete. Die gesuchte Strecke
l ist die unbekannte Kathete und es gilt:
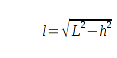 l
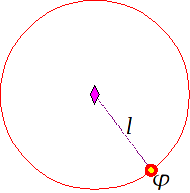
l ist der Ebenenabstand zwischen dem Bot und der Bake. Dieser ist aber ein Skalar und besitzt keine Richtungsinformation. Deshalb weiß der Bot auch nur, daß er sich irgendwo auf einem Kreis befindet, dessen Mittelpunkt die Bake ist und dessen Radius
l entspricht.
Analog werden die anderen beiden Ebenenabstände berechnet.
Die Länge des Vektors
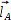
kann nun berechnet werden, jetzt fehlt nur noch die Winkelinformation.


 Die Konstruktion eines Hilfsdreiecks
Die Konstruktion eines Hilfsdreiecks
Über die Konstruktion eines Dreiecks aus drei Seitenlängen können dessen Winkel mit Hilfe des Kosinussatzes bestimmt werden.
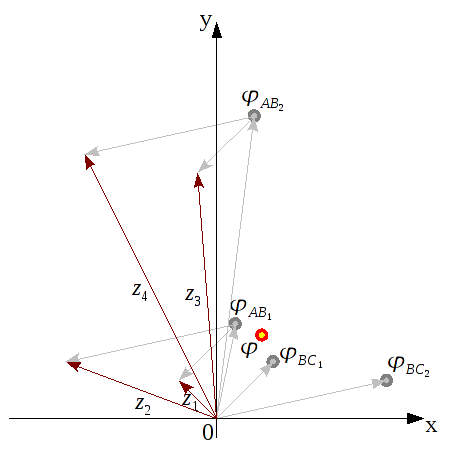
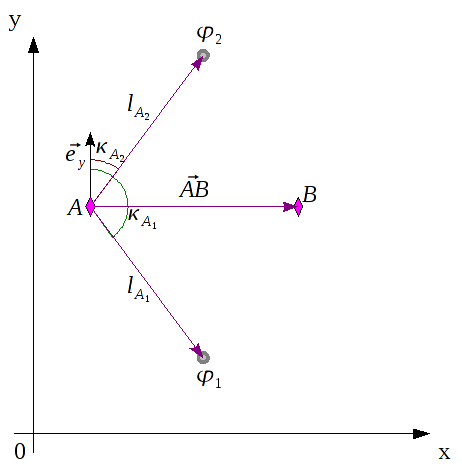
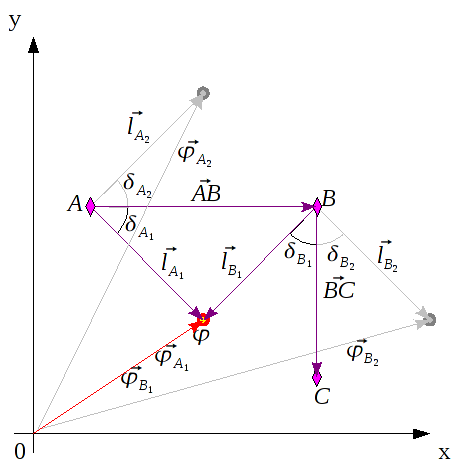
In der folgenden Abbildung habe ich bereits ein Hilfsdreieck aus den beiden Baken A und B, sowie der unbekannten Botposition φ gezeichnet. Mein φ kennt hier bisher aber nur die Ortsvektoren 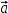 und
und 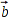 sowie die Abstände
sowie die Abstände 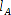 und
und 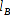 zu den Baken.
zu den Baken.
Die Seite AB muss erst noch bestimmt werden.
Aus der Grafik ist ersichtlich, daß
AB auch über den Vektor
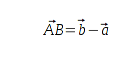
vollständig beschrieben ist, und deshalb kann
AB wie folgt berechnet werden.
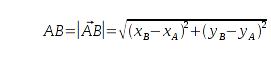
Jetzt sind alle drei Seitenlängen ermittelt und ich kann über den Kosinussatz den Winkel
δ berechnen.


 Das Problem der zwei Lösungen für die Winkelbestimmung
Das Problem der zwei Lösungen für die Winkelbestimmung
Nach dem Kosinussatz gilt für den Winkel δ:
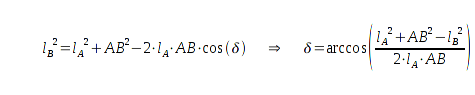
Leider lassen sich jedoch zwei Dreiecke aus den Seitenlängen AB, 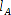 und
und 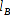 konstruieren.
konstruieren.
Somit habe ich aber zwei Winkel
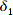
und
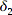
, für die offensichtlich gilt:
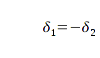
Für den Roboter bedeutet dies, daß er über den Kosinussatz nur

errechnen kann.
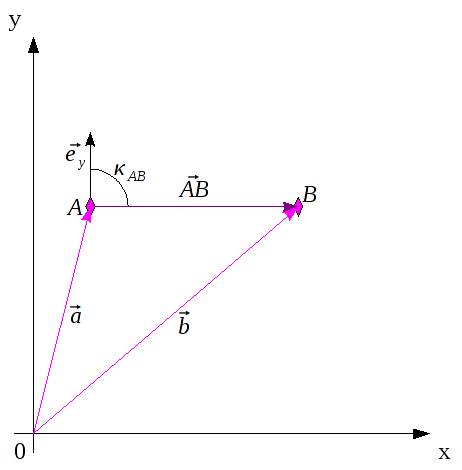
Da sich
δ auf den Vektor
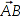
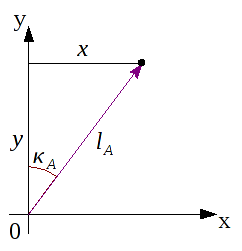
bezieht, muss auch dessen Winkelinformation bestimmt werden. Diese errechne ich über das
Skalarprodukt von
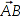
und dem Einheitsvektor
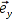
.
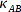
ist dabei der Winkel zwischen
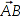
und der y-Achse.
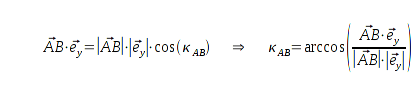
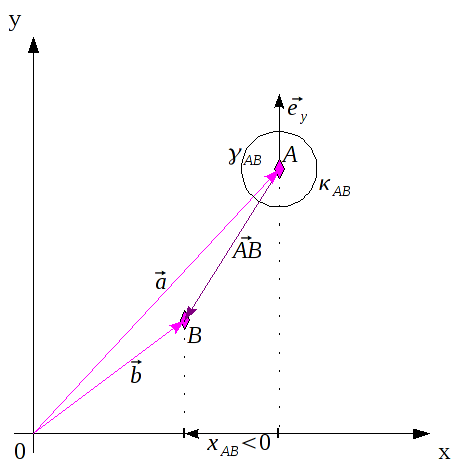
Bei dem Skalarprodukt darf eines nicht vergessen werden: Es wird immer der eingeschlossene Winkel berechnet, dieser ist immer ≤ 180°.
In der Grafik ist das der Winkel
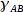
, benötigt wird allerdings
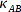
. Deshalb gilt: Ist die
x-Komponente des Vektors
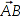 negativ
negativ, wird mit dem Skalarprodukt der kleinere Winkel
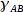
berechnet. Um Fehler auszuschließen, muss an dieser Stelle eine Fallunterscheidung gemacht werden. Wenn
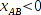
ist, wird
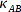
nach der folgenden Formel berechnet:
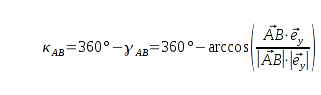
Aus den beiden Winkeln
δ und
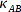
können nun zwei Lösungen für den absoluten Winkel
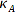
berechnet werden.
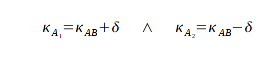
In der folgenden Grafik sind diese beiden Lösungen eingezeichnet. Sie sind offensichtlich spiegelsymetrisch zum Vektor
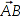
.
Analog zur
Koordinatentransformation von Polarkoordinaten in kartesische Koordinaten kann ich nun trigonometrisch die Vektoren
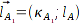
und
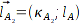
in kartesische Koordinaten überführen.
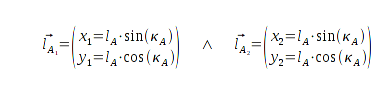
Diese Koordinatenpaare beziehen sich auf den Anfangspunkt
(0; 0). Erst die Summen dieser jeweils mit
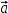
, ergeben die zwei möglichen Lösungen für den Ortsvektor
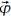
des Bots.
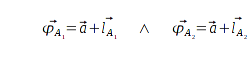


 Die Berechnung eines zweiten Lösungspaares
Die Berechnung eines zweiten Lösungspaares
Um die nicht mögliche Lösung auszuschließen, wird das Verfahren über ein weiteres Bakenpaar wiederholt, wobei es keine Rolle spielt, ob A oder B in diesem Paar enthalten sind. Deswegen reichen auch insgesamt drei Baken als Referenzen aus.
Der Einfachheit halber sei das zweite Hilfsdreieck über das Bakenpaar BC konstruiert:
Über
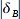
und das Skalarprodukt aus
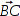
und
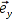
erhalte ich wieder die zwei Vektoren
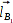
und
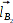
, sodaß sich nach der Transformation dann zwei weitere Lösungen für die Botposition ergeben und er nun vier mathematisch korrekte Ortsvektoren
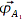
,
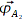
,
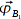
und
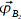
kennt.
Anschaulich logisch, daß der Ortsvektor, der über beide Bakenpaare gebildet wurde, der richtige sein muss.
Berechnen kann der Bot das wie folgt:


 Ausschluss der 'falschen' Lösungen
Ausschluss der 'falschen' Lösungen
Ich weiß, daß zwei Vektoren 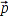 ,
, 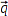 gleich sind, wenn ihre Differenz den Nullvektor
gleich sind, wenn ihre Differenz den Nullvektor 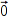 ergibt.
ergibt.
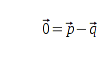
Demnach existieren theoretisch eine Gleichung und drei Ungleichungen, in diesem Fall:
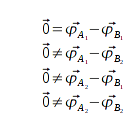
Daraus folgt unmittelbar
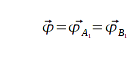
und damit wäre theoretisch die vektorielle Standortbestimmung eindeutig und abgeschlossen.
Praktisch wird es in annährend allen Fällen vier Ungleichungen geben. Dies resultiert aus kleinen, jedoch unvermeidbaren Fehlern bei den Abstandsmessungen und dem begrenzt genauen Algorithmus, der die anschließenden Berechnungen durchführt. Deshalb wird der Bot beim Subtrahieren der Lösungspaare vier Differenzvektoren 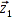 ,
, 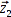 ,
, 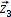 und
und 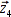 erhalten, die anschließend interpretiert werden müssen.
erhalten, die anschließend interpretiert werden müssen.
Was bedeuten die Differenzvektoren eigentlich? Sie zeigen von den Lösungen des zweiten Bakenpaars
BC auf die Lösungen des ersten Bakenpaars
AB, und damit sind ihre Beträge die Abstände zwischen den Lösungen.
Offenbar gilt, je kleiner

desto näher sind zwei Lösungen und desto wahrscheinlicher ist die Richtigkeit dieser. Das heißt wiederum, der Bot vergleicht nur noch die Beträge der Differenzvektoren, sucht sich den kleinsten Betrag heraus und nimmt einen der beiden zugehörigen Ortsvektoren als hinreichend genau an. In der Praxis sollte der Differenzvektor der
richtigen Lösung klein genug sein, um vernachlässigt zu werden.
Somit ist der kleinste Wert
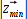
eine Aussage über die Güte der Messung. Ggf. kann der Bot auch
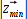
mit einer Konstante
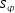
vergleichen und wenn gilt:
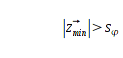
die Standortbestimmung als zu ungenau verwerfen und mit zwei günstigeren Bakenpaaren erneut den Standort berechnen, oder ggf. odometrisch eine bessere Position aufsuchen.
Übrigens kann man aus der Grafik ableiten, daß die vier Berechnungen, die die Differenzvektoren ergeben, ausreichen und sich die Vektoren bei Vertauschen der Baken zwar umkehren, ihre Beträge sich aber nicht verändern. Geometrisch bedeutet dies eine Punktspiegelung am Ursprung.


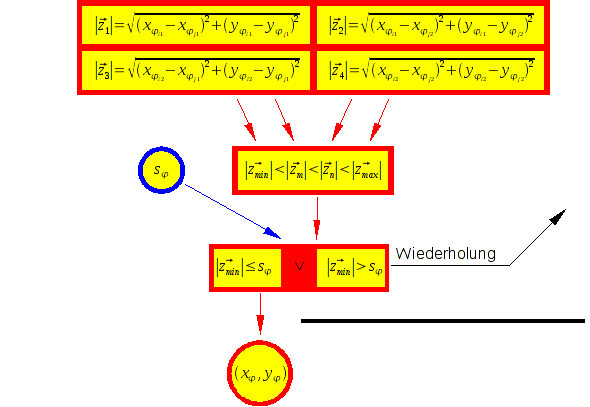
 Grafische Aufbereitung der Herleitung
Grafische Aufbereitung der Herleitung
Bekannt sind die Daten dreier Navigationsbaken und der Schwellwert, ab dem Messungen verworfen werden (blau umrahmt):
- Nav-Bake A: Position
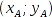 , Höhe
, Höhe 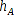 ;
;
- Nav-Bake B: Position
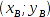 , Höhe
, Höhe 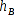 ;
;
- Nav-Bake C: Position
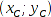 , Höhe
, Höhe 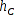 ;
;
- Schwellwert
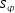 .
.
Gemessen werden die drei Abstände zu den Baken (grün markiert):
- Nav-Bake A: Abstand
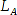 ;
;
- Nav-Bake B: Abstand
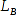 ;
;
- Nav-Bake C: Abstand
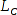 .
.
Zu berechnender Standort:
- Roboter φ: Position
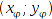
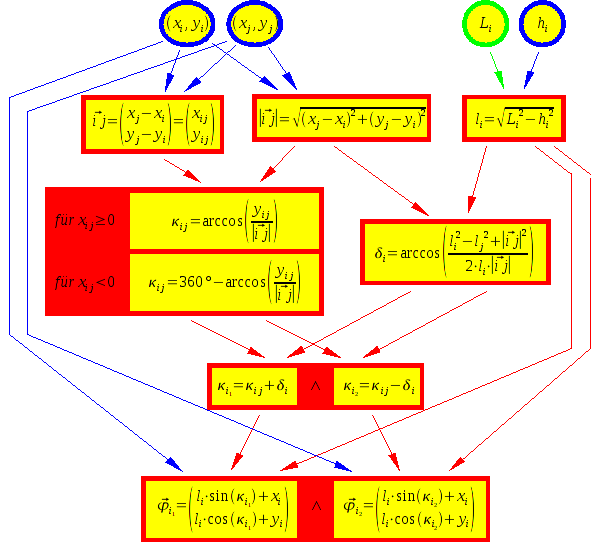
Die folgende Darstellung gibt einen Überblick über die notwendigen Berechnungen. Diese sind bereits vereinfacht und allgemein gehalten. Die neu eingeführten Variablen
i,
j verallgemeinern die Nav-Baken,
m,
n die Differenzvektoren.

 Eine Beispielrechnung
Eine Beispielrechnung
Die folgenden Anfangswerte sind durch eine Skizze abgeglichen worden, um eine geometrische Überprüfung machen zu können, und es hat gut funktioniert. Die hier gezeigten Ergebnisse sind gerundete Werte, die Berechnungen waren im Taschenrechner genauer.
- Nav-Bake A = (15; 65); Höhe
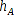 = 20; Abstand
= 20; Abstand 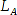 = 50,2;
= 50,2;
- Nav-Bake B = (60; 60); Höhe
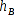 = 19; Abstand
= 19; Abstand 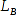 = 46,8;
= 46,8;
- Nav-Bake C = (55; 15); Höhe
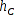 = 16; Abstand
= 16; Abstand 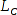 = 87,1;
= 87,1;
- Schwellwert
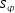 = 1
= 1
Zuerst werden die Ebenenabstände, Vebindungsvektoren der Bakenpaare, sowie die Bakenabstände berechnet.
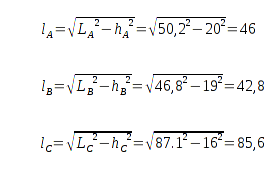
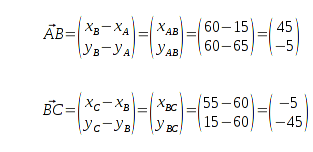
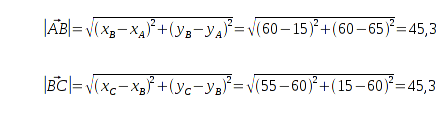
Dann werden die Winkel bestimmt. Für
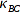
tritt auch gleich der Fall ein, daß über den Winkel
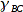
gerechnet werden muss.
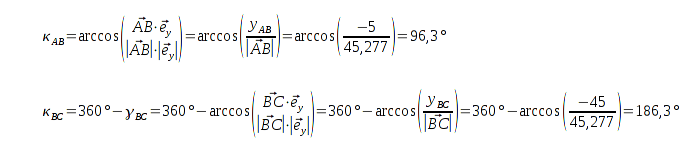
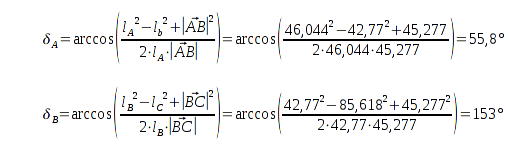
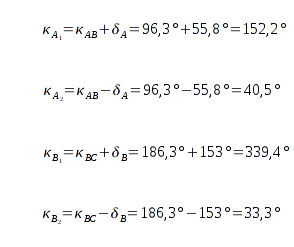
Die Überführung in kartesische Koordinaten läßt schon erkennen, was die richtige Lösung ist.
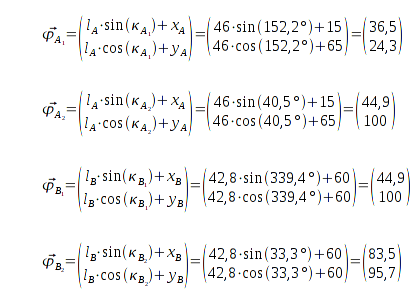
Gerundet ist es eindeutig, im Taschenrechner gibt es einige Stellen nach dem Komma Unterschiede, sodaß die Differenzvektoren es hier zwar nicht erkennen lassen, tatsächlich hat der Differenzvektor

aber einen Wert von ≈ 0,02.
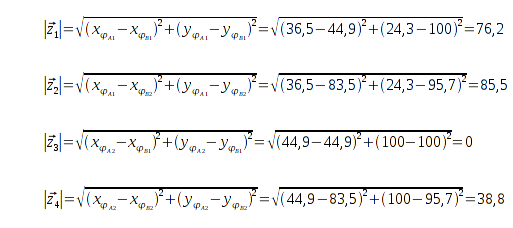
Da 0,02 <
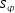
, wäre dies eine gute Positionsbestimmung, und der Bot wüßte jetzt, daß er hier steht:
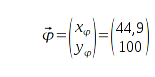
Geometrisch überprüft, ist diese Lösung richtig. Die Standortbestimmung ist hiermit eindeutig und abgeschlossen. Jetzt muss das nur noch der Roboter können.


![]() bestimmt hat, der vom Ursprung auf seine Position zeigt.
bestimmt hat, der vom Ursprung auf seine Position zeigt.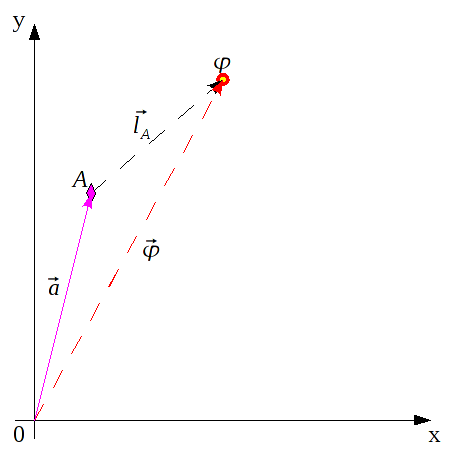
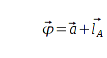
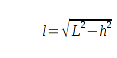
![]() und
und ![]() sowie die Abstände
sowie die Abstände ![]() und
und ![]() zu den Baken.
zu den Baken.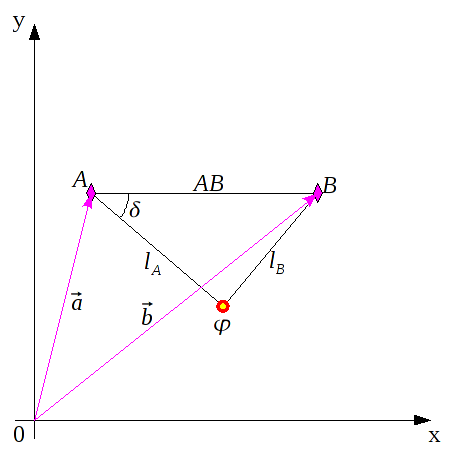
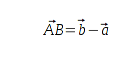
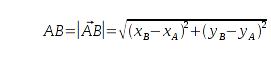
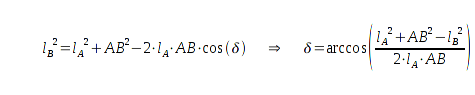
![]() und
und ![]() konstruieren.
konstruieren.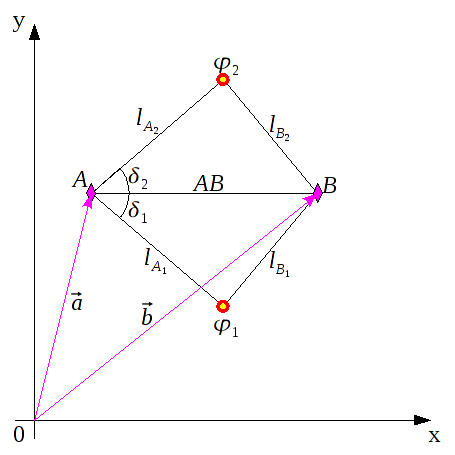
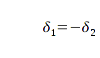
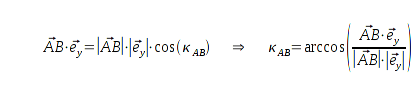
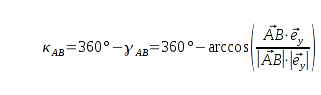
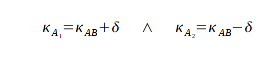
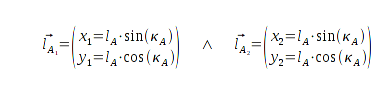
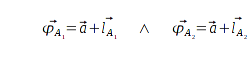
![]() ,
, ![]() gleich sind, wenn ihre Differenz den Nullvektor
gleich sind, wenn ihre Differenz den Nullvektor ![]() ergibt.
ergibt.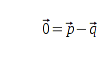
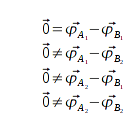
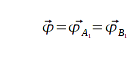
![]() ,
, ![]() ,
, ![]() und
und ![]() erhalten, die anschließend interpretiert werden müssen.
erhalten, die anschließend interpretiert werden müssen.